大多数结构工程师都知道,对于均匀载荷的梁,最大力矩发生在跨中,力矩值为 (w*l 2 )/8。对于中心的点载荷,最大力矩为 (P*l)/4。如果载荷不在中心,则最大力矩为 (P*a*b)/l,发生在点载荷的位置。对于三角形载荷,最大力矩位于 (√3 *l)/3,为 (√3 *w*l 2 )/27。
以下是我之前文中推导的函数。
计算均匀载荷:

计算点载荷:

计算三角载荷:

首先,我们来推导均匀载荷梁的最大力矩函数。
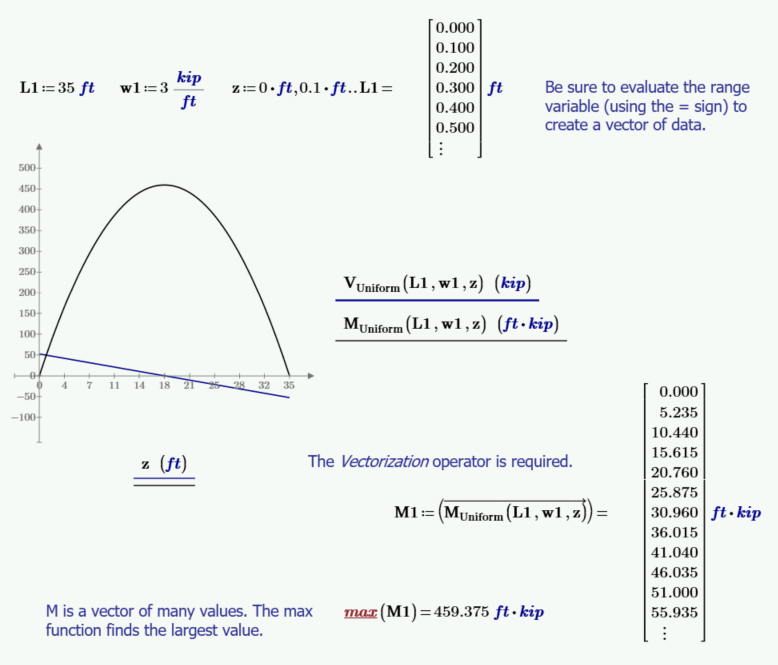
从下图中可以看出,最大力矩发生在剪力为零的位置。剪力等于力矩曲线的斜率,最大力矩点的斜率为零。
我们将使用数值数据绘制剪力和力矩图,然后使用这些数据来查找最大力矩。然后将这些数据与最大力矩的导出函数进行比较以进行检查。
请注意,需要使用矢量化运算符才能让 Mathcad 逐个元素执行计算。有关矢量化运算符的讨论,请参阅上一篇博客。最大
力矩的位置将以两种方式计算。第一种是使用导出的剪力函数并求解剪力为零的位置。第二种方法是对力矩函数求导以获得斜率函数(与剪力函数相同),然后求解零斜率的位置。导数运算符位于运算符部分的数学选项卡上。 零剪切(以及零斜率)的位置函数将用作矩函数中 x 的输入值,然后提供最大矩函数。
要推导出均匀载荷豆的最大力矩公式,请找到零剪切力的位置。使用符号求解关键字来查找零剪切力的位置。

使用上述数值的派生函数来检查最大矩函数。

推导点载荷的最大力矩函数。点载荷作用下的梁的最大力矩将发生在点载荷的位置。


使用M MaxPoint 函数推导出跨度中心点载荷的公式。

推导三角形载荷作用下的梁的最大弯矩函数。

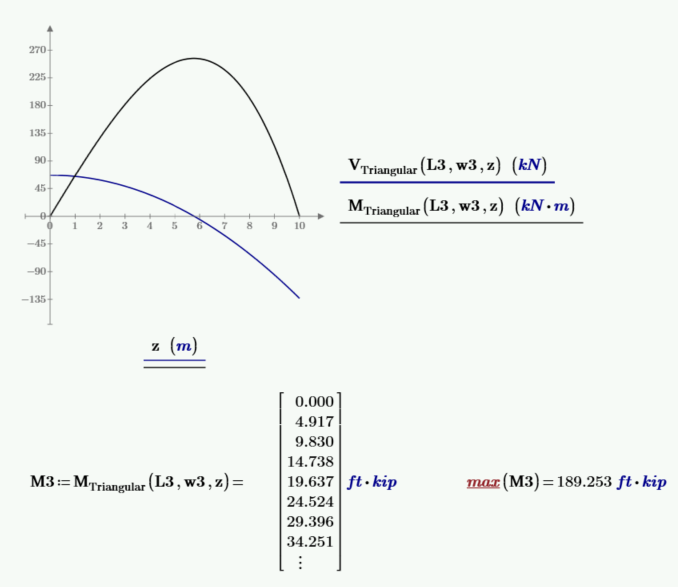

使用上述数值的派生函数来检查最大矩的结果。

在这篇博客中,我展示了如何使用 Mathcad 推导均匀载荷、点载荷和三角载荷下的简支梁的最大弯矩函数。这些示例说明:
- 函数的重要用途
- 使用带有关键字的符号求值运算符的威力
- 使用具有多条轨迹的 XY 图
- 定义绘图的范围变量
- 评估范围变量以创建值向量
- 使用矢量化运算符进行逐元素运算
- 使用导数算子计算曲线的斜率

